最长递增子序列 - O(nlogn)详解
话说最近刷到一道题目——最长递增子序列(简称LIS)。力扣上面有一个 O(nlogn) 的解法,但网站上面的题解似乎不是那么容易搞懂。因此,在这篇博客中我希望能彻头彻尾地把这道题目解释明白。
一、问题描述
给你一个整数数组nums,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7]是数组 [0,3,1,6,2,2,7]的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
二、 O(nlogn) 方法:
1. 耐心游戏
我们将通过学习一个纸牌游戏 - 耐心游戏来开始:
将一副牌 { c1, c2, …, cn } 根据以下两条规则分成任意几堆,问怎样才能让堆的数量最少。
- 无法将更大的牌放在更小的牌上面(比如不能把Q放在8上面)
- 如果上面的条件无法满足,可以重新另起一堆并将牌放在这堆上面。
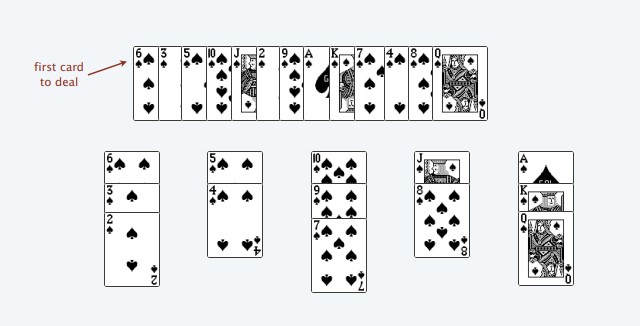
如上图所示,根据游戏规则我们不能将更大的牌放在更小的牌上面,所以每堆都是按降序排列的。但是我们可以另起一堆并在上面放上一张牌,这也就是为什么我们有 5 堆牌。
2. 耐心排序
那么,耐心排序的最优解是什么呢?
答案就是始终将卡片放在最左边符合规则堆上面。这个算法叫做耐心排序。
这是为啥?
耐心排序是一种贪心算法,这意味着它总是以每个阶段的局部最优解为目标。
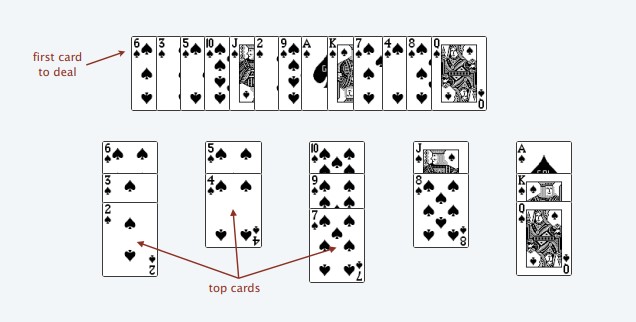
在耐心排序的任何阶段,牌堆的顶牌总是从左到右增加(顶牌就是一堆牌中最底下的牌,例如上图中的 2、4、7、8、Q就是顶牌)。将牌放在最左边符合规则的堆上,我们就选择了这步的局部最优解。
举个列子,假设我们有一套牌是 [10, 100, 5]。首先,我们将第一张黑桃10放入一堆。然后,因为我们无法将黑桃100放在黑桃10上,所以我们另起第二堆并将黑桃100放在上面(假设我们有黑桃100)。然而我们最后遇到了一个问题:应该把红桃5放在哪里?是放在第一堆,还是第二堆?

答案是我们应该把红桃5放在第一堆上。
如果我们把它放在第二堆,那么我们只能把牌数为1-9的(比如红桃4,黑桃9)放在第一堆,1-4放在第二堆。
然而,如果我们将其放在第一堆上,那么我们就可以将排数为1-4的放在第一堆上,1-99放在第二堆上。显然,这个选择为未来的牌预留了更多的“空间”,这就是为什么它是局部最优解。
3. 耐心排序和最长递增子序列
好的,现在我们知道耐心排序可以找到耐心游戏的最小堆数(最小牌堆的数量),但这与最长递增子序列(LIS)有何联系呢?因此,我们现在将证明耐心排序的最小堆数 = LIS 的长度。
引理 1:最小堆数 >= LIS 长度
证明:假设我们有一个最长递增子序列:c1 < c2 < ... < cn。
如果我们知道牌 c(i) 的位置,那么牌 c(i+1) 在哪里?
首先,c(i+1) 不可能和 c(i) 放在同一堆中,因为 c(i) 下面所有的牌都必须小于 c(i) 本身(游戏规则的设定)。
其次,c(i+1) 不能放在 c(i) 左边的一堆上,否则 c(i) 会放在那堆的上面(耐心排序原理)。
因此,我们知道牌 c(i+1) 一定位于 c(i) 右侧的某个堆中,这意味着LIS的长度至多就是耐心排序的最小堆数。
引理 2:最小堆数 <= LIS 的长度
证明:再次假设我们有一个 LIS:c1 < c2 < ... < cn。
首先我们考虑一张牌,c(i)。这张牌必须大于 c(i) 左侧牌堆上的顶牌 c(i-1),否则 c(i) 将被放入那堆的上面。然后我们来考虑 c(i-1),这张牌必须大于 c(i-1) 左侧的牌堆顶牌。因此我们可以看到,每堆中必定有一张牌可以连起来并形成递增顺序(但不一定是最长的,这就是为什么最小堆数最多是 LIS 的长度)。
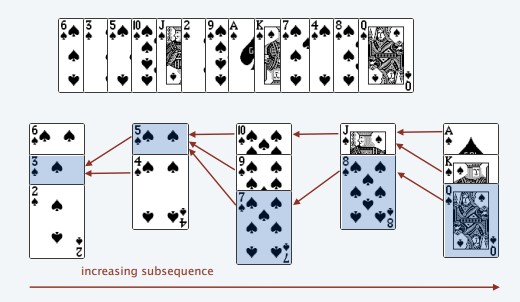
你有可能现在还是云里雾里的,所以我们来结合上面的图片来理解一下。
首先我们来考虑黑桃Q(最右面那张)。当它被放入牌堆时,它必须大于左边的顶牌,即黑桃8。否则,如果该牌小于8,则将会和黑桃8放在同一堆中。因此存在递增顺序,[8,10] 。
现在我们再来考虑黑桃8。当它被放入牌堆时,它必须大于左边最上面的一张牌,即黑桃7。因此存在递增顺序,[7, 8, Q]。
最后考虑黑桃7。当它放入牌堆时,它必须大于左边最上面的一张牌,即黑桃5(注意黑桃4是在黑桃7之后的,所以这里不被考虑)。因此,存在递增顺序, [5, 7, 8, Q]
…以此类推
我们可以看到每堆会有一张牌可以连起来形成递增顺序。[3, 5, 7, 8, Q]
因此:最小堆数 = LIS 的长度
通过以上两个引理,我们知道最小桩数必须等于 LIS 的长度才能同时满足两个引理。因此,最小堆数 = LIS 的长度。
4. 实现
好了,所以耐心排序的最少堆数 = LIS 的长度。我们现在该怎么实现呢?
我们可以模仿耐心排序的过程来求 LIS 的长度:
- 构建一个列表,
tails. 该列表将存储每堆的顶牌。 - 循环遍历
nums列表中的每个元素,就像我们发牌一样。 - 对于每个元素 x ,
tails将根据以下规则更新列表:
(1) 如果 x 大于tails中的所有元素,则将它append入tails。这一步就像耐心排序中另起一堆,并将牌放在上面一样。
(2) 如果tails[i-1]< x <=tails[i],则用 x 更新tails[i]。这一步就像将一张牌放在现有的一堆上。
注意这个步骤是用二分搜索完成的,因为我们可以使用二分搜索来找到元素 x 该放位置。 tails的长度就是最小堆数,也就是LIS的长度。
假如我们有nums = [4,5,6,3],那么tails就会像这样增加:
[4]
[4, 5]
[4, 5, 6]
[3, 5, 6]
5. 总结
我们nums中每个元素循环的一遍,并对于每个元素我们都使用了一次二分搜索来查找它应该放入的位置,所以大 O 就是 O(nlogn)。
6. 注脚
这里是这篇文章英文版。
三、C++ 代码
根据思路写的代码:
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int i, j, size = 0;
int tails[nums.size()];
for (int x : nums) {
i = 0, j = size;
// 二分搜索
while (i != j) {
int m = (i + j) / 2;
if (tails[m] < x) i = m + 1;
else j = m;
}
tails[i] = x; // 要么更换tails[i],要么添加
size = max(i + 1, size); // 更新长度
}
return size;
}
};
或者一个更短,使用C++库函数的代码:
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int size = 0;
for(auto num : nums)
if (size == 0 || nums[size - 1] < num) nums[size++] = num;
else *lower_bound(nums.begin(), nums.begin() + size, num) = num;
return size;
}
};