Longest Increasing Subsequence - O(nlogn) Solution

Recently I have encountered a problem - Longest Increasing Subsequence(LIS). There’s an O(nlogn) solution, but after some searching I haven’t found a statisfying explaination. Hence in this blog I wonder if I could explain it clearly but also thoroughly.

1. Problem Description

Given an integer array nums, return the length of the longest strictly increasing subsequence.

Examples:

Example 1:

Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

Example 2:

Input: nums = [0,1,0,3,2,3]
Output: 4

Example 3:

Input: nums = [7,7,7,7,7,7,7]
Output: 1

2. O(nlogn) Solution

2.1 Patience Game

It may seem a bit odd, but we will begin the solution by learning a traditional card game - the Patience Game:
Deal cards c1, c2, …, cn into piles according to two rules:

• Can’t place a higher-valued card onto a lowered-valued card.
• Can form a new pile and put a card onto it.

The goals is to have the minimal number of piles.

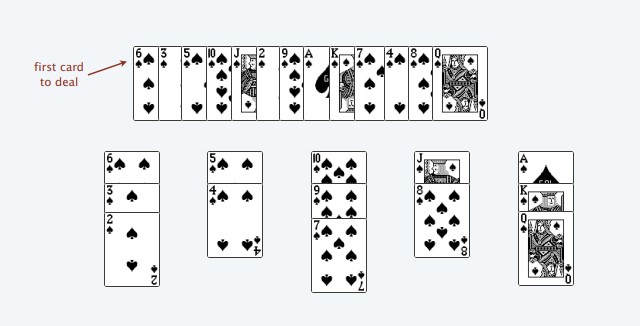
Shown in the picture above, each pile is in descending order, since we can’t place a higher valued card onto a lowered value card. However, we can form a new pile and put a card onto it, which is why we have 5 different piles.

2.2 Patience Sort

So, how do we optimise this?
The answer is to always place the card on the left-most pile that is valid. This algorithm is called Patience Sort.

How does this work?
Patience Sort is a greedy algorithm, which means that it always aims for the locally optimal choice at each stage.

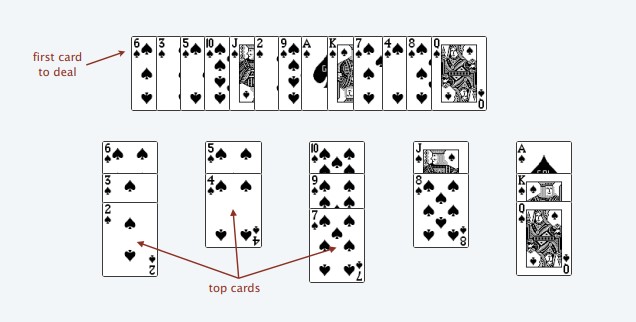
At any stage during greedy algorithm, top cards of the piles always increase from left to right. (Top card is the bottom-most card in a pile, such as 2, 4, 7, 8, Q in the image above). By placing it on the left-most pile that is valid, we have chosen the optimal choice at this stage.

For example, imagine we have a card set that is [10, 100, 5]
First, we place 10 of spades into a pile. Then, we make a second pile and place 100 of spades on it, since we can’t place the 100 on the 10.
At last, we encounter the 5 of hearts. Where do we place the 5 of hearts? On the first pile, with 10 of spades, or the second pile, with 100 of spades?

We should place 5 of hearts onto the first pile.
If we place it on the second pile, then we can only place 1-9 in the first pile, and 1-4 on the second one.
However, if we place it on the first pile, then we can place 1-4 on the first pile, and 1-99 on the second one. It is obvious that this option provides more ‘room’ for future cards, which is why it is the local optimal solution.

2.3 Patience Sort and LIS

OK, so Patience Sort finds the minimal number of piles to play the Patience Game. But how does this link with Longest Increasing Subsequence(LIS)? Hence in this section we are going to prove that minimal number of piles = length of LIS (the strong duality of the two).

Lemma 1: minimal number of piles >= length of LIS
Proof: Assume we have an LIS: c1 < c2 < ... < cn.
If we know a card c(i), where is card c(i+1)?
First, c(i+1) cannot be in the same pile as c(i), since all cards on top of c(i) must be smaller than c(i) itself.
Second, c(i+1) cannot be placed on a pile left of c(i), otherwise c(i) would be placed in that pile(According to Patience Sort).
Hence, we know that a card c(i+1) must be in some pile to the right of c(i).
This means that the length of LIS is at most the minimal number of piles.

Lemma 2: minimal number of piles <= length of LIS
Proof: Again, assume we have an LIS: c1 < c2 < ... < cn.
Consider a card, c(i). This card must be greater than the top card, c(i-1), on the pile to the left of c(i), otherwise c(i) would be put in that pile. Now consider c(i-1). This card must be greater than the top card on the pile to the left of c(i-1). Hence we can see that there must a card from each pile that forms an Increasing Order (though not necessarily the longest, which is why the minimal number of piles is at most the length of LIS).

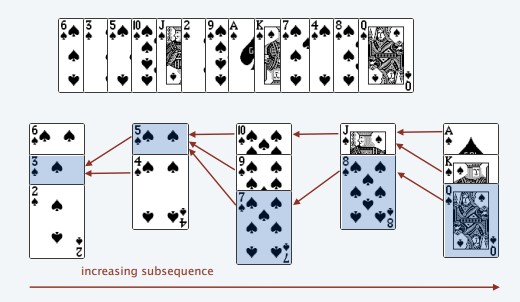
Look at the the image above.
Consider the Q of spades. When it is placed on the pile, it must be greater than the top card on the left, which is 8 of spades. Otherwise, if the card is smaller than 8, then it would be put of the same pile as 8 of spades. Hence there’s an Increasing Order, [8, Q]
Consider the 8 of spades. When it is placed on the pile, it must be greater than the top card on the left, which is 7 of spades. Hence there’s an Increasing Order, [7, 8, Q]
Consider the 7 of spades. When it is placed on the pile, it must be greater than the top card on the left, which is 5 of spades. Hence there’s an Increasing Order, [5, 7, 8, Q]. Notice that 4 of spades is placed after 7 of spades, so we do not consider it now.
… and so on
We can see there’s a card from each pile that forms an Increasing Order, [3, 5, 7, 8, Q].

Overall: minimal number of piles = length of LIS
By combining <= and >=, we know that the minimal number of piles must equal to the length of LIS in order to satisfy both lemmas. Hence minimal number of piles = length of LIS.

2.4 Implementation

OK, so minimal number of piles = length of LIS. What do we do now?
We can just mimic the process of Patience Sort to find the length of LIS:

1. Construct a list, tails. This list will store the top cards in each pile.

2. Loop through each element in the nums list, just like we are dealing each card.

3. For each element x, update the tails list based on the rules below:

   (1) If x is larger than all the elements in tails, append it. This step is like creating a new pile.
   (2) If tails[i-1] < x <= tails[i], update tails[i] with x. This step is like putting a card on an existing pile.

   Note that this step is completed using Binary Search, since we can use Binary Search to loop throught tails and find the appropriate position for element x.

4. The length of the tails list is the number of piles, which is also the length of LIS.

For example, if we have nums = [4,5,6,3], then the tails list increases like this:

[4]
[4, 5]
[4, 5, 6]
[3, 5, 6]

2.5 Conclusion

Overall, we have iterated through nums once, and for every element we have used Binary Search once, so the Big O would be O(nlogn).

Voila! This is the O(nlogn) solution, with the Python implementation appended below. Thanks for reading this much.

3. C++ Solutions

3.1 Solution #1

Standard implementation:

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int i, j, size = 0;
        int tails[nums.size()];

        for (int x : nums) {
            i = 0, j = size;
            // Binary Search
            while (i != j) {
                int m = (i + j) / 2;
                if (tails[m] < x) i = m + 1;
                else j = m;
            }
            // Either update tails[i] with num, or append num
            tails[i] = x; 
            // Update the length of LIS
            size = max(i + 1, size); 
        }

        return size;
    }
};

Time Complexity: O(nlogn)
Space Complexity: O(n)

3.2 Solution #2

A shorter piece of code:
(Using C++ built-in function lower_bound for Binary Search and the input array itself as the tails list)

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int size = 0;
        for(auto num : nums) 
            if (size == 0 || nums[size - 1] < num) nums[size++] = num;
            else *lower_bound(nums.begin(), nums.begin() + size, num) = num;
        return size;
    }
};

Time Complexity: O(nlogn)
Space Complexity: O(1)

4. Bibiliography

• https://leetcode.com/problems/longest-increasing-subsequence/
• https://en.wikipedia.org/wiki/Patience_sorting
• https://www.cs.princeton.edu/courses/archive/spring13/cos423/lectures/LongestIncreasingSubsequence.pdf
• https://www.youtube.com/watch?v=22s1xxRvy28