kiwirafe.blog
Home Archive 中文站

Simhash Algorithm Explained

Simhash is a text similarity algorithm proposed by Moses Charikar in his paper “Similarity Estimation Techniques from Rounding Algorithms”. There are many explanations of this algorithm online, but in this blog I want to dig into the depth of the algorithm and find out why this algorithm actually works.

1. Procedure

Let’s start with the procedure of Simhash.

  1. Filter the Corpus: This includes sentence extraction, stop words removal, word segmentation, etc.

  2. Calculate the Weights: Calculate the weight (e.g., TF-IDF) of each word in the corpus. Select the top words with the highest TF-IDF values. For example, if , the selected words and their TF-IDF values would be:

    Simhash: 1
text: 2
similarity: 3

  3. Hash Each Word: Hash each word into an bit binary number using a hash function such as SHA-256 or MD5. You’ll soon see that the hash function doesn’t matter here. Using the same example in Step 2, the words and their corresponding hash values would be:

    Simhash: 100
text: 010
similarity: 011

  4. Replace Bits with Weights: For each word, replace each bit of its hash value with its weight (positive if the bit is 1, negative if the bit is 0):

    Simhash: [1, -1, -1]
text: [-2, 2, -2]
similarity: [-3, 3, 3]

  5. Sum the Values: Sum the values in each bit position.

    1 + (-2) + (-3) = -4
(-1) + 2 + 3 = 4
(-1) + (-2) + 3 = 0

Result: [-4, 4, 0]

  6. Generate the Fingerprint: Convert the summed values into a binary fingerprint. If a bit is positive or zero, replace it with 1; otherwise, replace it with 0.

    [-4, 4, 0] -> 010

    This fingerprint represents the corpus “Simhash text similarity”.

  7. Calculate Similarity: After we find the fingerprints for two documents, we can use Hamming Distance to calculate the distance or similarity between these documents. Hamming Distance essentially just counts up the number of different bits in two documents. If we want a similarity within [0, 1], we can count the number of bits that are the same, then divide it by the total number of bits.

The full process is summarized by the following image.

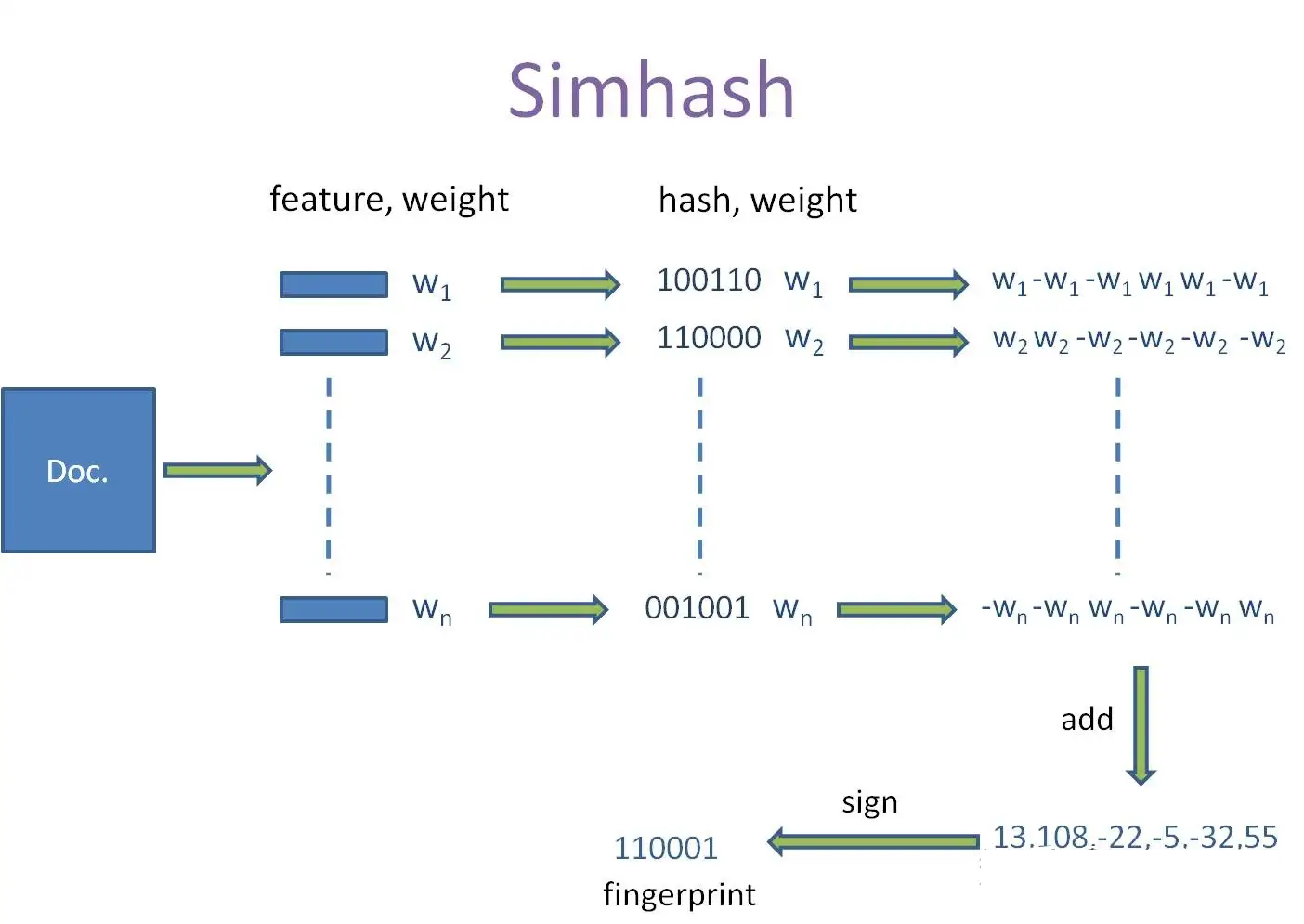
simhash-tutorial-1-img-2

2. Algorithm

2.1 The Theory

Simhash was proposed by Moses Charikar in his paper “Similarity Estimation Techniques from Rounding Algorithms”. In the paper, he raised the key concept that Simhash is an algorithm that estimates Cosine Similarity.

Let’s assume we have a random hyperplane (a hyperplane is essentially a plane in dimensions). Since a hyperplane is also a kind of plane, we know it must have two sides. We define one side as 1, and the other as 0.

Which side is 1, which side is 0?

We know that a hyperplane is defined by its normal vector . Hence we define the side that aligns the direction of the normal vector as 1. If a vector has a positive dot product with , it lies on the same side as and we assign it 1; otherwise, we assign it 0.

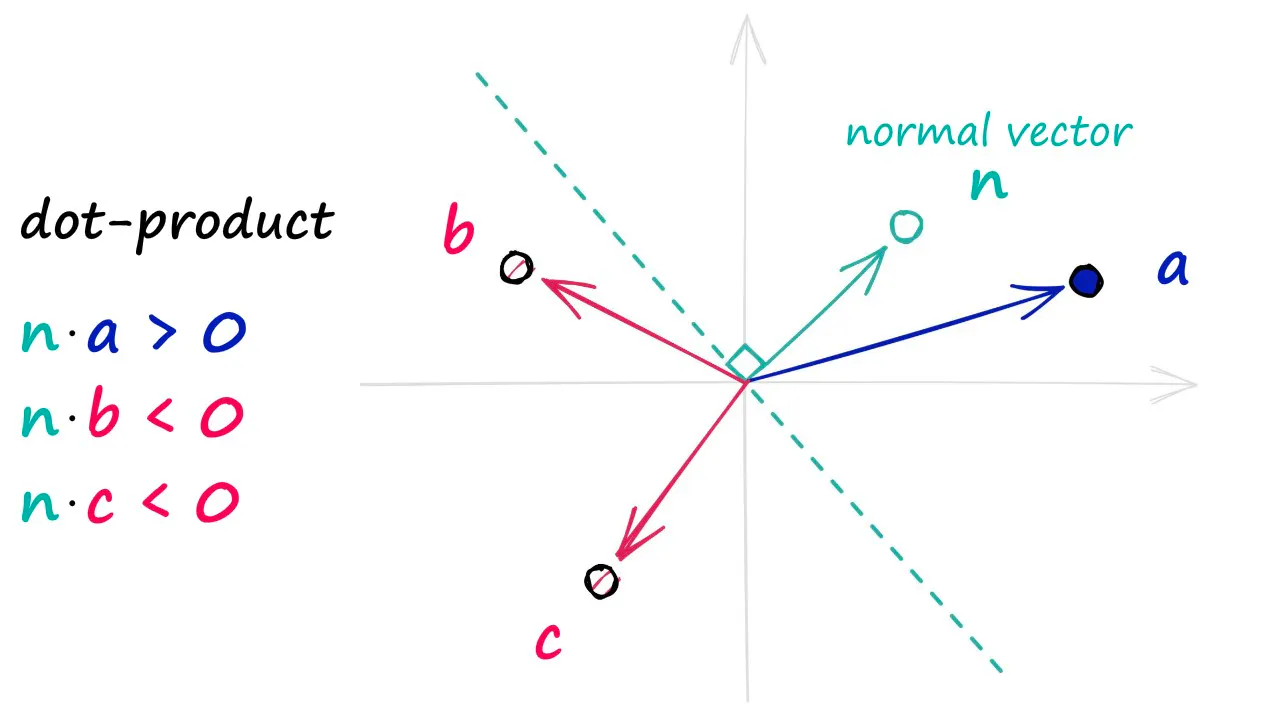
simhash-tutorial-1-img-2

In Charikar’s paper, Simhash is defined as follows:

This is the same as what we described above, expect in this case represents the normal vector.

Now, what is the probability that two vectors are on different sides of a hyperplane?

Two vectors are only on different sides of a hyperplane if the hyperplane is in between them, ie. cutting the angle () between them. Hence the probability that the hyperplane cuts the angle between them is 2 times the size of the angle divided by 360 degrees (2 times since the direction of the hyperplane doesn’t matter). Mathematically,


On the opposite hand, what is the probability that two vectors are on the same side of a hyperplane?

This is simple. It’s just 1 minus the probability calculated above. Mathematically,

If we look at this carefully, we can see that this is proportional to Cosine Similarity. Specially, the ratio between and is at least 0.87856.

2.2 In Practice

We can see that Simhash estimates Cosine Similarity. However, how does all the math in Part 2.1 correlate to the procedure in Part 1?

The hash values from Step 3 in Part 1 are as follows:

Simhash: 100
text: 010
similarity: 011

Let’s look vertically:

1 | 0 | 0
0 | 1 | 0
0 | 1 | 1

We can treat hash functions (such as SHA-256) as random number generators. Futhermore, the randomness is enhanced by using only one bit per hashed number (since we are examining the bits vertically). Therefore, a vector composed of bits from different hashed strings can be considered random. This process effectively generates the normal vectors () of the random hyperplanes.

So we have three random vectors:

[1 0 0]
[0 1 1]
[0 0 1]

Then, we replace 0 with -1.

[1 -1 -1]
[-1 1 1]
[-1 -1 1]

In Part 2.2, we perform a dot product between and . This is analogous to Step 4 in Part 1, where we essentially perform a dot product between the weight vector () and the three random vectors (multiple hyperplanes’ normals ). This can be treated as matrix multiplication, where the matrix is composed of the three random vectors, and it is multiplied by the weight vector.

Recall your matrix multiplication:

Tada! The result is the same as what we calculated in Step 5.

Finally, we apply Charikar’s definition:

And the final fingerprint is 110 as well!

2.3 Conclusion

After all the explanation above, I hope you see the correlation between theory and practice. First, we hashed the words to get a series of random vectors. Second, we dot multiplied the random vectors with the weight vector. Third, we applied Charikar’s definition to generate the fingerprint. This ensured that the for two fingerprints, the probability that two bits are the same is proportional to Cosine Similarity. Finally, we can use Hamming Distance to approximate the similarity between two texts.

3. Implementation

3.1 Installation

Xiangsi is a Pypi library designed for text similarity, and we will be using that to implement Simhash similarity. We can install xiangsi with pip:

pip3 install xiangsi

3.2 Code

Calculating Simhash is easy as two lines of code:

import xiangsi as xs
xs.simhash("A mathematician found a solution to the problem.", "The problem was solved by a young mathematician.")

4. Futher Reading

Futher reading on Simhash Algorithm - FAQs that answers the following four questions:

  1. What value should we choose for ?
  2. Why do we need multiple random hyperplanes?
  3. Why are we not using random vectors?
  4. How to use textsim?

5. Bibliography