Enshadowed - NZIC 2023 Round 3 Tutorial

This problem comes from New Zealand Olympiad in Informatics (NZOI) 2023 Round 3. For the problem statement refer to here: Enshadowed.

This problem requires an understanding of Dijkstra’s algorithm plus some extra mathematical knowledge. I was quite surprised about this because this problem was the 3rd question in the round, and usually question 3 is more about standard algorithms (Greedy, DP, etc). Now let’s walk through this problem in detail.

1. Algorithm

1.1 Circles

The first concept to understand is that it is always optimal to walk to the centre of the circle, or not walk in the circle at all.

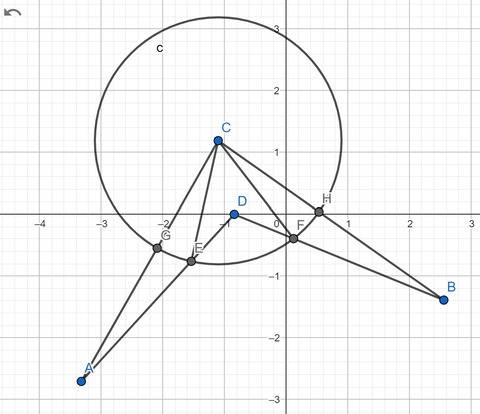
Let us consider the graph above: Points A and B are random points out of Circle C; C is the centre of the circle; Point E is somewhere in the circle. Since distance that we walk in the circle doesn’t matter, we only have to prove that AG and AE, and BH < BF.

Proof
Since AE + CE > AC (Sides of a triangle)
Hence AE + CE > AG + CG
Hence AE > AG (CG = CE = Radius)
Similarly, BH < BF

Thus we have proven that it is always optimal to walk to the centre of the circle. However, we might not have to walk into the circles at all. This is when AB < AG + BH. Therefore, as I have mentioned at the start of this section, we either walk to the center of the circle, or not walk into the circle at all.

1.2 Dijkstra’s Algorithm

However, there are multiple trees that we can walk to. Which trees should we walk? Which order should we walk? Should we walk into the trees at all? The answer to these questions is Dijkstra’s Algorithm (which I assume you are familiar with).

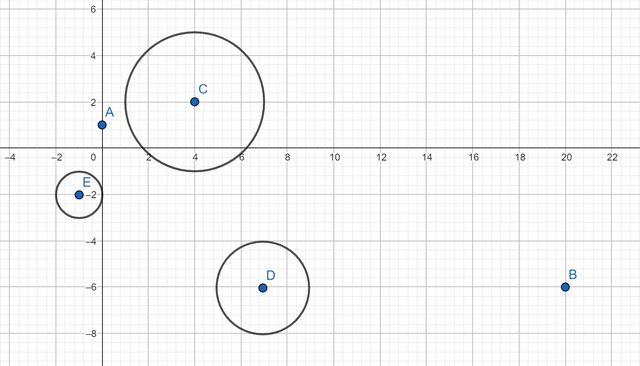
Now let’s consider the second example from the problem statement (shown in image above). The most optimal solution is A->C->D->B. We treat the startig point(Roxy’s current position, A) and the ending point(her destination, B) along with every circle’s center(C, D, E) as a node, and their paths between each other as edges. The weights of the edges are the distance between the nodes, minus the radius of the circles. Then we just simply run Dijkstra’s Algorithm to find the shortest path from A to B, which is our answer to the problem.

A few implementation tips:

Use priority queue to implement Dijkstra’s Algorithm to keep time complexity as O(n + mlogm).
Append the starting point and the ending point as nodes with radius 0.

1.3 Time Complexity

The construction of the graph is , as we loop through each pair of nodes to find their distances between them.
The Dijkstra’s Algorithm is , since the number of edges is:

Hence the overall Time Complexity is .

1.4 Conclusion

Personally I think this problem is quite hard, which I have spent a few days trying to figure out a solution. I started with a greedy approach, but when I began the Shortest Path direction, I came together with an answer quite quickly.

2. C++ Solution

#include <bits/stdc++.h>
using namespace std;

#define euclid(x1, x2, y1, y2) sqrt(pow(x2 - x1, 2) + pow(y2 - y1, 2))

// Dijkstra's Algorithm
// Be cautious to use double since the problem can have decimals.
double dijkstra(int source, int target, vector<pair<int, double>> *adj, int n) {
    double distance[n];
    bool processed[n];
    for(int i = 0; i < n; i++){
        distance[i] = INT_MAX;
        processed[i] = false;
    }

    priority_queue<pair<double, int>> q;
    distance[source] = 0;
    q.push({0, source});
    while(!q.empty()) {
        int a = q.top().second; q.pop();
        if(processed[a]) continue;
        processed[a] = true;
        for(auto u : adj[a]) {
            int b = u.first; double w = u.second;
            if (distance[a] + w < distance[b]) {
                distance[b] = distance[a] + w;
                q.push({-distance[b], b});
            }
        }
    }

    return distance[target];
}

int main() {
    double x1, y1, r1, x2, y2, r2, xq, yq, rq;
    int N;

    cin >> x1 >> y1 >> x2 >> y2;
    cin >> N;

    vector<tuple<double, double, double>> circles;
    for (int i = 0; i < N; i++) {
        cin >> xq >> yq >> rq;
        circles.push_back({xq, yq, rq});
    }

    // Add the the starting and ending nodes.
    circles.push_back({x1, y1, 0});
    circles.push_back({x2, y2, 0});

    // Calculate the distance between the nodes.
    vector<pair<int, double>> adj[N + 2];
    for (int i = 0; i < N + 2; i++) {
        for (int j = 0; j < N + 2; j++) {
            tie(x1, y1, r1) = circles[i];
            tie(x2, y2, r2) = circles[j];
            // Euclid is defined earlier.
            adj[i].push_back({j, max(euclid(x1, x2, y1, y2) - r1 - r2, 0.0)});
        }
    }

    double distance = dijkstra(N, N + 1, adj, N + 2);

    // Return 6dp due to problem requirement.
    printf("%.6f\n", distance);
    
}